深入理解HashMap底层原理

HashMap作为Java集合类重要的元素之一，其蕴含的精妙代码设计，除了在工作中经常用到之外，也是面试中常见的考点。普通的程序员，可能仅仅能说出HashMap线程不安全，允许key、value为null，以及不要求线程安全时，效率上比HashTable要快一些。稍微好一些的，会对具体实现有过大概了解，能说出HashMap由数组+链表+RBT实现（JDK8），并了解HashMap的扩容机制。如果你有刨根问底的激情，那么你肯定想知道它具体是如何实现的。

本文将从下几个方面进行剖析：HashMap的结构、put方法、get方法、remove方法、resize方法。

以下HashMap源码基于JDK 8

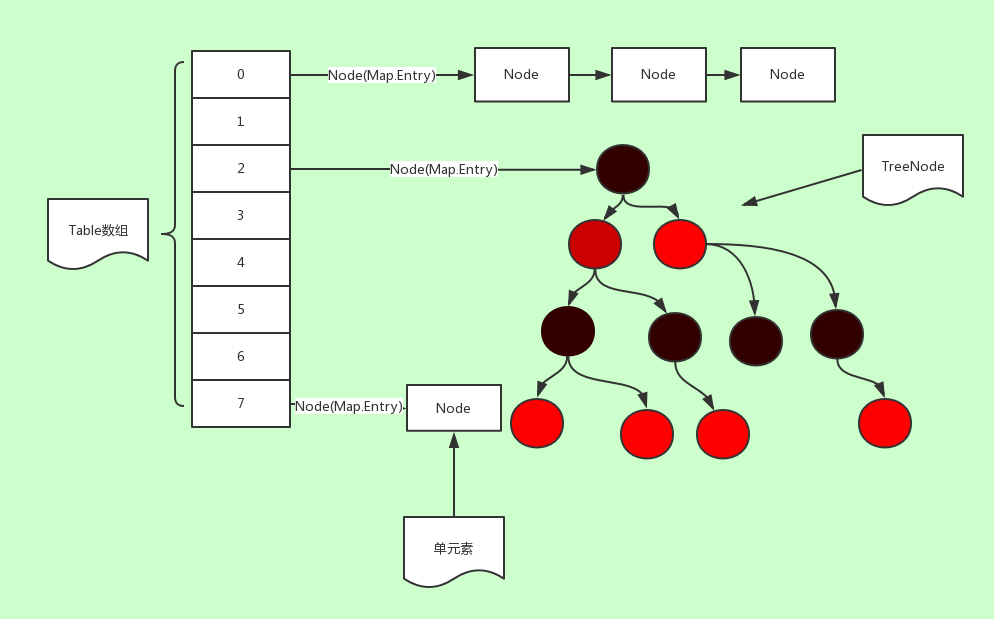
HashMap结构

JDK1.8 以前HashMap的实现是：数组+链表

JDK1.8 开始HashMap的实现是：数组+链表+红黑树

如下图：

强烈推荐一个数据结构可视化的网站：

Data Structure Visualizations

这里先了解HashMap的几个核心成员变量：

/**
* 默认初始容量16 （必须是2的倍数）
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16 

/**
 *  最大容量为2的30次方
 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/**
 * 默认加载因子0.75（结合时间和空间效率考虑得到的）
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 * 树形阈值：JDK 1.8 新增的，当使用`树`而不是`列表`来作为桶时使用。必须比2大
 * （也就是：当put一个元素时，其链表长度达到8时将链表转换为红黑树。）
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * 非树形阈值：也是 1.8 新增的，扩容时分裂一个树形桶的阈值，要比TREEIFY_THRESHOLD小
 * （即：链表长度小于6时，红黑树会转成链表。）
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * 默认的最小的扩容量64：桶可能是树的哈希表的最小容量。至少为4 * TREEIFY_THRESHOLD=32，即默认初始容量的2倍
 */
static final int MIN_TREEIFY_CAPACITY = 64;

为什么TREEIFY_THRESHOLD的默认值被设定为8？HashMap中有这样一段注释：

* Because TreeNodes are about twice the size of regular nodes, we
* use them only when bins contain enough nodes to warrant use
* (see TREEIFY_THRESHOLD). And when they become too small (due to
* removal or resizing) they are converted back to plain bins.  In
* usages with well-distributed user hashCodes, tree bins are
* rarely used.  Ideally, under random hashCodes, the frequency of
* nodes in bins follows a Poisson distribution
* (http://en.wikipedia.org/wiki/Poisson_distribution) with a
* parameter of about 0.5 on average for the default resizing
* threshold of 0.75, although with a large variance because of
* resizing granularity. Ignoring variance, the expected
* occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
* factorial(k)). The first values are:
*
* 0:    0.60653066
* 1:    0.30326533
* 2:    0.07581633
* 3:    0.01263606
* 4:    0.00157952
* 5:    0.00015795
* 6:    0.00001316
* 7:    0.00000094
* 8:    0.00000006
* more: less than 1 in ten million

理想情况，在随机哈希码下，容器中的节点遵循泊松分布（Poisson），按照泊松分布的计算公式计算出了链表中元素个数和概率的对照表，可以看到链表中元素个数为8时的概率已经非常小。

另一方面红黑树平均查找长度是log(n)，长度为8的时候，平均查找长度为3，如果继续使用链表，平均查找长度为8/2=4，这才有转换为树的必要。链表长度如果是小于等于6，6/2=3，虽然速度也很快的，但是链表和红黑树之间的转换也很耗时。选择6和8，中间还有个差值7可以有效防止链表和树频繁转换。

再看下另外的几个成员变量：

//HashMap的哈希桶数组，用于存放表示键值对数据的Node元素。
transient Node<K,V>[] table;

//HashMap将数据转换成set的另一种存储形式，这个变量主要用于迭代功能。
transient Set<Map.Entry<K,V>> entrySet;

//HashMap中实际存在的Node数量，注意这个数量不等于table的长度，甚至可能大于它，因为在table的每个节点上是一个链表（或RBT）结构，可能不止有一个Node元素存在。
transient int size;

//HashMap的数据被修改的次数，这个变量用于迭代过程中的Fail-Fast机制，其意义在于保证发生了线程安全问题时，能及时的发现（操作前备份的count和当前modCount不相等）并抛出异常(ConcurrentModificationException)终止操作。
transient int modCount;

//HashMap的扩容阈值，在HashMap中存储的Node键值对超过这个数量时，自动扩容容量为原来的二倍。
int threshold;

//HashMap的负载因子，可计算出当前table长度下的扩容阈值：threshold = loadFactor * table.length。 
final float loadFactor;

显然，HashMap的底层实现是基于一个Node的数组，其是HashMap的一个内部类：

static class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;

    Node(int hash, K key, V value, Node<K,V> next) {
        this.hash = hash;
        this.key = key;
        this.value = value;
        this.next = next;
    }

    public final K getKey()        { return key; }
    public final V getValue()      { return value; }
    public final String toString() { return key + "=" + value; }

    public final int hashCode() {
        return Objects.hashCode(key) ^ Objects.hashCode(value);
    }

    public final V setValue(V newValue) {
        V oldValue = value;
        value = newValue;
        return oldValue;
    }

    public final boolean equals(Object o) {
        if (o == this)
            return true;
        if (o instanceof Map.Entry) {
            Map.Entry<?,?> e = (Map.Entry<?,?>)o;
            if (Objects.equals(key, e.getKey()) &&
                Objects.equals(value, e.getValue()))
                return true;
        }
        return false;
    }
}

它实现了Map.Entry接口，内部的变量含义也很明确，hash值、key/value对和实现链表和红黑树所需要的指针索引。

HashMap内部定义的几个变量，包括桶数组本身都是transient修饰，这代表了他们无法被序列化，而HashMap本身是实现了Serializable接口的。
这很容易产生疑惑：HashMap是如何序列化的呢？查了源码发现，HashMap内有两个用于序列化的函数 readObject(ObjectInputStream s) 和 writeObject（ObjectOutputStreams），通过这个函数将table序列化。

put方法解析

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,              //这里onlyIfAbsent表示只有在该key对应原来的value为null的时候才插入，也就是说如果value之前存在了，就不会被新put的元素覆盖。
               boolean evict) {                                             //evict参数用于LinkedHashMap中的尾部操作，这里没有实际意义。
    Node<K,V>[] tab; Node<K,V> p; int n, i;                                 //定义变量tab是将要操作的Node数组引用，p表示tab上的某Node节点，n为tab的长度，i为tab的下标。
    if ((tab = table) == null || (n = tab.length) == 0)                     //判断当table为null或者tab的长度为0时，即table尚未初始化，此时通过resize()方法得到初始化的table。             　　　　　　　
        n = (tab = resize()).length;                                      　//这种情况是可能发生的，HashMap的注释中提到：The table, initialized on first use, and resized as necessary。
    if ((p = tab[i = (n - 1) & hash]) == null)                              //此处通过（n - 1） & hash 计算出的值作为tab的下标i，并另p表示tab[i]，也就是该链表第一个节点的位置。并判断p是否为null。
        tab[i] = newNode(hash, key, value, null);                           //当p为null时，表明tab[i]上没有任何元素，那么接下来就new第一个Node节点，调用newNode方法返回新节点赋值给tab[i]。
    else {                                                                  //下面进入p不为null的情况，有三种情况：p为链表节点；p为红黑树节点；p是链表节点但长度为临界长度TREEIFY_THRESHOLD，再插入任何元素就要变成红黑树了。
        Node<K,V> e; K k;                                                   //定义e引用即将插入的Node节点，并且下文可以看出 k = p.key。
        if (p.hash == hash &&                                               //HashMap中判断key相同的条件是key的hash相同，并且符合equals方法。这里判断了p.key是否和插入的key相等，如果相等，则将p的引用赋给e。
            ((k = p.key) == key || (key != null && key.equals(k))))         //这一步的判断其实是属于一种特殊情况，即HashMap中已经存在了key，于是插入操作就不需要了，只要把原来的value覆盖就可以了。
            e = p;                                                          //这里为什么要把p赋值给e，而不是直接覆盖原值呢？答案很简单，现在我们只判断了第一个节点，后面还可能出现key相同，所以需要在最后一并处理。
        else if (p instanceof TreeNode)                                     //现在开始了第一种情况，p是红黑树节点，那么肯定插入后仍然是红黑树节点，所以我们直接强制转型p后调用TreeNode.putTreeVal方法，返回的引用赋给e。
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); //你可能好奇，这里怎么不遍历tree看看有没有key相同的节点呢？其实，putTreeVal内部进行了遍历，存在相同hash时返回被覆盖的TreeNode，否则返回null。
        else {                                                              //接下里就是p为链表节点的情形，也就是上述说的另外两类情况：插入后还是链表/插入后转红黑树。另外，上行转型代码也说明了TreeNode是Node的一个子类。
            for (int binCount = 0; ; ++binCount) {                          //我们需要一个计数器来计算当前链表的元素个数，并遍历链表，binCount就是这个计数器。
                if ((e = p.next) == null) {                                 //遍历过程中当发现p.next为null时，说明链表到头了，直接在p的后面插入新的链表节点，即把新节点的引用赋给p.next，插入操作就完成了。注意此时e赋给p。
                    p.next = newNode(hash, key, value, null);               //最后一个参数为新节点的next，这里传入null，保证了新节点继续为该链表的末端。(查看newNode方法可知)
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st    //插入成功后，要判断是否需要转换为红黑树，因为插入后链表长度加1，而binCount并不包含新节点，所以判断时要将临界阈值减1。
                        treeifyBin(tab, hash);                              //当新长度满足转换条件时，调用treeifyBin方法，将该链表转换为红黑树。
                    break;                                                  //当然如果不满足转换条件，那么插入数据后结构也无需变动，所有插入操作也到此结束了，break退出即可。
                }
                if (e.hash == hash &&                                       //在遍历链表的过程中，我之前提到了，有可能遍历到与插入的key相同的节点，此时只要将这个节点引用赋值给e，最后通过e去把新的value覆盖掉就可以了。
                    ((k = e.key) == key || (key != null && key.equals(k)))) //老样子判断当前遍历的节点的key是否相同。
                    break;                                                  //找到了相同key的节点，那么插入操作也不需要了，直接break退出循环进行最后的value覆盖操作。
                p = e;                                                      //在第21行我提到过，e是当前遍历的节点p的下一个节点，p = e 就是依次遍历链表的核心语句。每次循环时p都是下一个node节点。
            }
        }
        if (e != null) { // existing mapping for key                        //左边注释为jdk自带注释，说的很明白了，针对已经存在key的情况做处理。
            V oldValue = e.value;                                           //定义oldValue，即原存在的节点e的value值。
            if (!onlyIfAbsent || oldValue == null)                          //前面提到，onlyIfAbsent表示存在key相同时不做覆盖处理，这里作为判断条件，可以看出当onlyIfAbsent为false或者oldValue为null时，进行覆盖操作。
                e.value = value;                                            //覆盖操作，将原节点e上的value设置为插入的新value。
            afterNodeAccess(e);                                             //这个函数在hashmap中没有任何操作，是个空函数，他存在主要是为了linkedHashMap的一些后续处理工作。
            return oldValue;                                                //这里很有意思，他返回的是被覆盖的oldValue。我们在使用put方法时很少用他的返回值，甚至忘了它的存在，这里我们知道，他返回的是被覆盖的oldValue。
        }
    }
    ++modCount;                                                             //收尾工作，值得一提的是，对key相同而覆盖oldValue的情况，在前面已经return，不会执行这里，所以那一类情况不算数据结构变化，并不改变modCount值。
    if (++size > threshold)                                                 //同理，覆盖oldValue时显然没有新元素添加，除此之外都新增了一个元素，这里++size并与threshold判断是否达到了扩容标准。
        resize();                                                           //当HashMap中存在的node节点大于threshold时，hashmap进行扩容。
    afterNodeInsertion(evict);                                              //这里与前面的afterNodeAccess同理，是用于linkedHashMap的尾部操作，HashMap中并无实际意义。
    return null;                                                            //最终，对于真正进行插入元素的情况，put函数一律返回null。
}

在上述代码中的第十行，HashMap根据 (n - 1) & hash 求出了元素在node数组的下标。这个操作非常精妙，下面我们仔细分析一下计算下标的过程，主要分三个阶段：计算hashcode、高位运算和取模运算。

首先，传进来的hash值是由put方法中的hash(key)产生的（上述第2行），我们来看一下hash()方法的源码：

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

这里通过key.hashCode()计算出key的哈希值，然后将哈希值h右移16位，再与原来的h做异或^运算——这一步是高位运算。设想一下，如果没有高位运算，那么hash值将是一个int型的32位数。而从2的-31次幂到2的31次幂之间，有将近几十亿的空间，如果我们的HashMap的table有这么长，内存早就爆了。所以这个散列值不能直接用来最终的取模运算，而需要先加入高位运算，将高16位和低16位的信息”融合”到一起，也称为”扰动函数”。这样才能保证hash值所有位的数值特征都保存下来而没有遗漏，从而使映射结果尽可能的松散。最后，根据 n-1 做与操作的取模运算。

这里也能看出为什么HashMap要限制table的长度为2的n次幂，因为这样，n-1可以保证二进制展示形式是（以n=16为例）0000 0000 0000 0000 0000 0000 0000 1111。在做”与”操作时，就等同于截取hash二进制值得后四位数据作为下标。这里也可以看出”扰动函数”的重要性了，如果高位不参与运算，那么高16位的hash特征几乎永远得不到展现，发生hash碰撞的几率就会增大，从而影响性能。

HashMap的put方法的源码实现就是这样了，整理思路非常连贯。这里面有几个函数的源码（比如resize、putTreeValue、newNode、treeifyBin）限于篇幅原因，就不贴了，有兴趣的同学也可以自己挖掘一下。

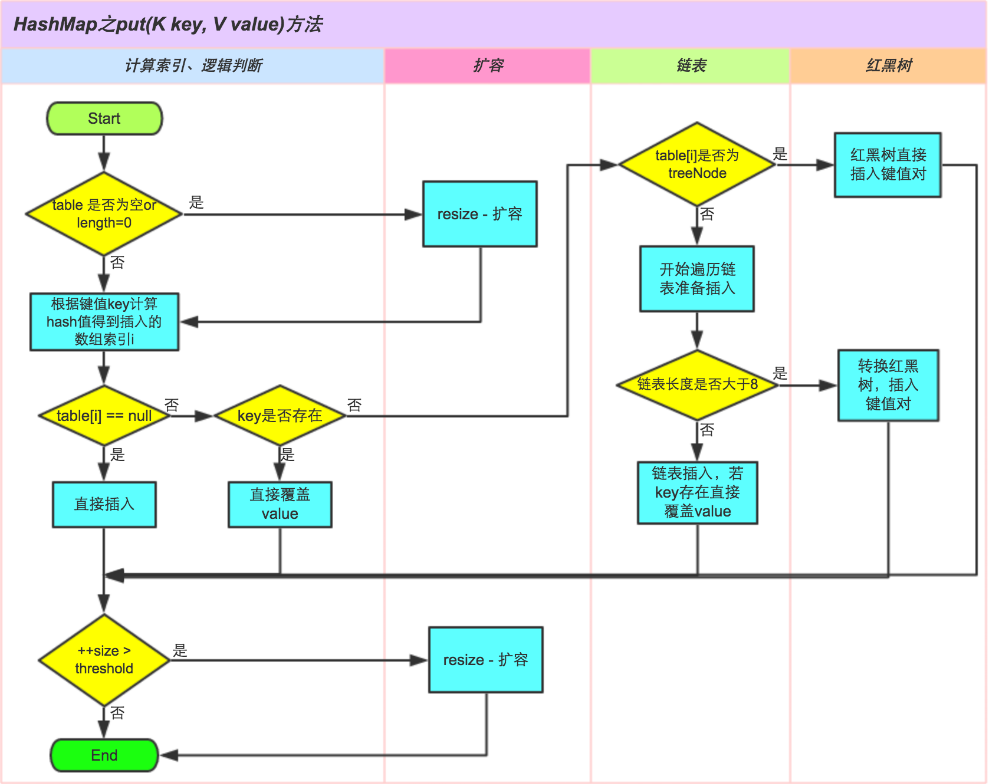
附上put方法简易流程图，辅助理解：

get方法解析

读完了put的源码，其实已经可以很清晰的理清HashMap的工作原理了。接下来再看get方法的源码，就非常的简单：

public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;          //根据key及其hash值查询node节点，如果存在，则返回该节点的value值。
}

final Node<K,V> getNode(int hash, Object key) {                             //根据key搜索节点的方法。记住判断key相等的条件：hash值相同 并且 符合equals方法。
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    if ((tab = table) != null && (n = tab.length) > 0 &&                    //根据输入的hash值，可以直接计算出对应的下标（n - 1）& hash，缩小查询范围，如果存在结果，则必定在table的这个位置上。
        (first = tab[(n - 1) & hash]) != null) {
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))     //判断第一个存在的节点的key是否和查询的key相等。如果相等，直接返回该节点。
            return first;
        if ((e = first.next) != null) {                                     //遍历该链表/红黑树直到next为null。
            if (first instanceof TreeNode)                                  //当这个table节点上存储的是红黑树结构时，在根节点first上调用getTreeNode方法，在内部遍历红黑树节点，查看是否有匹配的TreeNode。
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
                if (e.hash == hash &&                                       //当这个table节点上存储的是链表结构时，用跟第11行同样的方式去判断key是否相同。
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);                                 //如果key不同，一直遍历下去直到链表尽头，e.next == null。
        }
    }
    return null;
}

因为查询过程不涉及到HashMap的结构变动，所以get方法的源码显得很简洁。核心逻辑就是遍历table某特定位置上的所有节点，分别与key进行比较看是否相等。

remove方法解析

public V remove(Object key) {
    Node<K,V> e;
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
        null : e.value;
}

/**
  * 1.寻找是否存在,如果存在分数据类型分别处理
  * 2.如果为树,稍微复杂一点,需要判断是否要转换成链表,然后就是树的移动
  */
final Node<K,V> removeNode(int hash, Object key, Object value,
                           boolean matchValue, boolean movable) {
    Node<K,V>[] tab; Node<K,V> p; int n, index;
    //找到节点
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (p = tab[index = (n - 1) & hash]) != null) {
        Node<K,V> node = null, e; K k; V v;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            node = p;
        //从树节点获取，待删除元素在桶中，但不是桶中首元素
        else if ((e = p.next) != null) {
            // 待删除元素在红黑树结构的桶中
            if (p instanceof TreeNode)
                // 查找红黑树
                node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
            else {
                // 遍历链表，查找待删除元素
                do {
                    if (e.hash == hash &&
                        ((k = e.key) == key ||
                         (key != null && key.equals(k)))) {
                        node = e;
                        break;
                    }
                    // p保存待删除节点的前一个节点，用于链表删除操作
                    p = e;
                } while ((e = e.next) != null);
            }
        }
        /**
         * matchValue为true：表示必须value相等才进行删除操作
         * matchValue为false：表示无须判断value，直接根据key进行删除操作
         */
        if (node != null && (!matchValue || (v = node.value) == value ||
                             (value != null && value.equals(v)))) {
            // 桶为红黑数结构，删除节点
            if (node instanceof TreeNode)
                // movable参数用于红黑树操作
                ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
            // 待删除节点是桶链表表头，将子节点放进桶位
            else if (node == p)
                tab[index] = node.next;
            // 待删除节点在桶链表中间
            else
                p.next = node.next;
            ++modCount;
            --size;
            afterNodeRemoval(node);
            return node;
        }
    }
    // 待删除元素不存在，返回null
    return null;
}

resize方法解析

扩容时机：

1. 当为空的时候,也就是没有初始化的时候
2. 当到达最大值时候
3. 普通扩容时候

final Node<K,V>[] resize() {
    //保存旧的 Hash 数组
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    //存在旧值
    if (oldCap > 0) {
        //超过最大容量，不再进行扩充，最大容量设置为2<<32 - 1
        if (oldCap >= MAXIMUM_CAPACITY) {
            //不移动.,没有空间移动
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        //容量没有超过最大值，属于正常范围的扩容 容量 x2
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            //阀值变为原来的两倍
            newThr = oldThr << 1; // double threshold
    }
    //用户自己设定了初始化大小
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    //如果没使用,使用默认值初始化
    else {               // zero initial threshold signifies using defaults
         //阀值和容量使用默认值
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    //用户自定义了map的初始化操作
    if (newThr == 0) {
        //计算新的阀值
        float ft = (float)newCap * loadFactor;
        //阀值没有超过最大阀值，设置新的阀值
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
     //新的容量
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    //创建新的 Hash 表
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    //如果是扩容操作，遍历旧的 Hash 表
    if (oldTab != null) {
        // 遍历map的数据，把每个bucket都移动到新的bucket中
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                //释放空间
                oldTab[j] = null;
                //如果当前位置只有一个元素,直接移动到新的位置
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                 //如果是红黑树
                else if (e instanceof TreeNode)
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                //如果没超过8个 是链表
                else { // preserve order
                    // 链表优化重hash的代码块
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                     //此处的操作是这样子的 因为是扩容一倍的操作,所以与旧的容量进行与操作后只有两个值0 和 1
                    //如果是0就位置不变,如果是1就移动n+old的位置,
                    //个人认为这么做的好处是:
                    /**
                     * 1.不会像之前1.7发生循环依赖的问题
                     * 2.从概率的角度上来看可以均匀分配,(一般来说高位和低位比例差不多)
                     * 3.提高效率
                     */
                    do {
                        next = e.next;
                        //如果和旧容量位运算后的值是0,记得当前节点和存放在链表的尾部
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        // 原索引+oldCap
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                     // 原索引放到bucket里
                     //为0的还是存放在当前位置
                    if (loTail != null) {
                        //最后一个节点的下一个节点做空
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    // 原索引+oldCap放到bucket里
                    if (hiTail != null) {
                        //最后一个节点的下一个节点做空
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

Java8在扩容后重新计算位置的时候,对链表进行优化,有兴趣可以搜索一下HashMap导致cpu百分之百的问题。而在Java中通过巧妙的进行&操作，然后获得高位是为0还是1，最终移动的位置就是低位的链表留在原地，高位的放在index+oldsize的地方就可以了。不用为每一个元素计算hash值,然后移动到对应的位置，再判断是否是链表，是否需要转换成树的操作。

JDK 7以前的HashMap相关实现原理，和JDK 8以后还是有点区别的，可参考：

JDK 7关于HashMap的实现原理

写在最后

问：HashMap如果确定只装载100个元素，new HashMap(?)多少是最佳的，为什么?

HashMap有两个参数影响其性能：初始容量和加载因子，前文我们已经分析了相关的代码。当哈希表中条目的数目超过容量乘加载因子的时候，则要对该哈希表进行resize扩容操作，从而哈希表将具有大约两倍的桶数。HashMap默认的加载因子是0.75，它在时间和空间成本上寻求了一种折中。

回到本文的问题。如果这个只装载100个元素的HashMap没有特殊的用途，那么为了在时间和空间上达到最佳性能，HashMap的初始容量可以设为：

100/0.75 = 133.33，为了防止resize，向上取整，为134。

但是还有另外一个问题，就是hash碰撞的问题。如果我们将HashMap的容量设置为134，那么如何保证其中的哈希碰撞会比较少呢？除非重写hashcode()方法，否则，似乎没有办法保证。

Put方法的第10行代码处，也给出了HashMap如何为元素选择下标的方法：p = tab[i = (n - 1) & hash])。hash为key哈希后得到的值，n为哈希表的长度。

134-1 = 128 + 6 -1；

假设这100个装载的元素中他们的key在哈希后有得到两个值（h），他们的二进制值除了低3位之外都相同，而第一个值的低3位为011，第二个值的低3位为001；

这时候进行java的&预算，011 & 101 = 001 ；001 & 101 = 001；他们的值相等了，那么这个时候就会发生哈希碰撞。

除此之外还有一个更加严重的问题，由于在101中第二位是0，那么，无论我们的key在哈希运算之后得到的值h是什么，那么在&运算之后，得到的结果的倒数第二位均为0；

因此，对于hash表所有下标的二进制的值而言，只要低位第二位的值为1，（例如0010,0011,0111,1111）那么这个下标所代表的桶将一直是空的，因为代码中的&运算的结果永远不会产生低位第二位为1的值。这就大大地浪费了空间，同时还增加了哈希碰撞的概率。这无疑会降低HashMap的效率。

那么如何才能减少这种浪费呢？最佳的方法当然是让length-1的二进制值全部位均为1。那么多少合适呢？没错，length=2^n，只要将hash表的长度设为2的N次方，那么，所有的哈希桶均有被使用的可能。

再次验证了HashMap要限制table的长度为2的n次幂的一个原因

回到刚才问题，与134最靠近的2^n无疑是128。但是100/128=0.78，已经超过默认加载因子的大小了。HashMap会进行resize操作，变成256。所以最好的结果还是256。

补充：在Java中，无论你的HashMap(x)中的x设置为多少，HashMap的大小都是2^n。2^n是大于x的第一个数。

参考文章：

深入Java集合学习系列：HashMap的实现原理
Java8 HashMap源码分析
java 8 Hashmap深入解析—put get 方法源码
在元素的装载数量明确的时候HashMap的大小应该如何选择